“The simplest way to model
a radiating body is to regard it as a large number of linear oscillators (on the
order of 1023) performing simple harmonic
motion. Since the particles undergoing the oscillations are, in general,
charged particles, they will radiate electromagnetic waves. In the case of a
cavity in thermal equilibrium, the electromagnetic energy
density inside the cavity will equal the energy density of the atomic
oscillators situated in the cavity walls. When the walls are raised to a higher
temperature, the following events take place: more energy is put into existing
oscillator modes by increasing their amplitudes, new modes corresponding to
stiffer spring constants (higher frequencies) are excited, and the radiation
density in the cavity is increased until a new equilibrium point is reached.”
--Elmer E. Anderson, from page 45 of Modern Physics and Quantum Mechanics, published in 1971 by W. B. Saunders
Company. It’s a good textbook, but I must confess I slightly edited this quotation. I didn't edit the last sentence, and for me that's the main explanatory part of the quote. My copy
of the book is a complimentary copy sent by the publisher to Oswald F. “Mike” Schuette of
the Physics & Astronomy Department at the U. of South Carolina. Professor
Schuette died in 2000, thus allowing graduate students like me to obtain books
from his office. We were given permission by Schuette’s family and the department, and it was
suggested that we take any books we wanted, first come first served. I got five or six books, including the transcript of J. Robert Oppenheimer's security hearings of 1954.
What I like about Elmer's description is that he says increasing the temperature of the box puts more energy into existing modes and creates new modes at higher frequencies.
I mentioned in my previous post that a mode is almost the same thing as a single frequency, but not quite. The standing waves in the box, which are also called resonant frequencies or normal modes, are determined by the dimensions of the box. The same idea in one dimension is shown by standing waves on a piece of string tied at both ends--a guitar or violin string for instance. These are the normal modes of the string and are determined by the length of the string. A single integer, usually expressed by our old friend n, multiplied by the speed of the waves on the string and divided by the twice the length of the string, determines the normal mode frequencies: f = n(v/2L).
To put it in the language of music, when n=1 we have the fundamental frequency, and for n > 1 we have the harmonics. All the different strangely shaped waveforms produced by musical instruments and other sound sources are made of a linear superposition of pure tones--the fundamental and its harmonics--having different amplitudes. Mathematically, we're talking about Fourier analysis.
The same idea applies to light waves in the Planck box, but we have three integers because we have three dimensions, and a mode is determined by the different values these integers can have, ranging from zero to infinity. And the speed v in the equation above is now c, the speed of light. Our equation for the allowed frequencies is then a little more complicated:
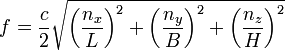
where L, B and H are the box's dimensions in the x, y and z directions, respectively. For a light wave there are two independent polarizations that result in twice as many possible modes.
All of the above is classical physics, not quantum physics. Planck's quantization of the energy of the waves is where the quantum of quantum mechanics comes in: E = nhf, where E is energy, f is frequency, h is Planck's constant, and n is an integer that is now called "the number of photons in the mode." So when we say more energy is put into a mode, increasing its amplitude, that means n increases but f remains the same.
In addition, as Mr. Dr. Anderson says, new modes corresponding to higher frequencies are "excited" when the box is heated to a higher temperature.
Can there be different modes with the same energy? Yes. To use easy-to-write frequencies, let's say we have two photons in a mode of frequency 100,000,000 Hz and one photon in a mode of frequency 200,000,000 Hz in our box. These modes of oscillation of the EM field in the box have the same energy but different frequencies.
The quantum world would not be so mysterious if it only meant energy is found to exist in discrete quantities rather than as a continuum. What makes the quantum world mysterious is that these discrete-energy entities that we would normally call particles interfere with each other like waves, and this interference is a result of there being a certain probability of finding, say, a photon in a particular place. The interference of probability amplitudes is what makes quantum mechanics weird! More on that later, since it's a bit off our current subject of the Planck radiation box.
What I like about Elmer's description is that he says increasing the temperature of the box puts more energy into existing modes and creates new modes at higher frequencies.
I mentioned in my previous post that a mode is almost the same thing as a single frequency, but not quite. The standing waves in the box, which are also called resonant frequencies or normal modes, are determined by the dimensions of the box. The same idea in one dimension is shown by standing waves on a piece of string tied at both ends--a guitar or violin string for instance. These are the normal modes of the string and are determined by the length of the string. A single integer, usually expressed by our old friend n, multiplied by the speed of the waves on the string and divided by the twice the length of the string, determines the normal mode frequencies: f = n(v/2L).
To put it in the language of music, when n=1 we have the fundamental frequency, and for n > 1 we have the harmonics. All the different strangely shaped waveforms produced by musical instruments and other sound sources are made of a linear superposition of pure tones--the fundamental and its harmonics--having different amplitudes. Mathematically, we're talking about Fourier analysis.
The same idea applies to light waves in the Planck box, but we have three integers because we have three dimensions, and a mode is determined by the different values these integers can have, ranging from zero to infinity. And the speed v in the equation above is now c, the speed of light. Our equation for the allowed frequencies is then a little more complicated:
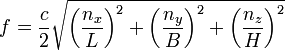
where L, B and H are the box's dimensions in the x, y and z directions, respectively. For a light wave there are two independent polarizations that result in twice as many possible modes.
All of the above is classical physics, not quantum physics. Planck's quantization of the energy of the waves is where the quantum of quantum mechanics comes in: E = nhf, where E is energy, f is frequency, h is Planck's constant, and n is an integer that is now called "the number of photons in the mode." So when we say more energy is put into a mode, increasing its amplitude, that means n increases but f remains the same.
In addition, as Mr. Dr. Anderson says, new modes corresponding to higher frequencies are "excited" when the box is heated to a higher temperature.
Can there be different modes with the same energy? Yes. To use easy-to-write frequencies, let's say we have two photons in a mode of frequency 100,000,000 Hz and one photon in a mode of frequency 200,000,000 Hz in our box. These modes of oscillation of the EM field in the box have the same energy but different frequencies.
The quantum world would not be so mysterious if it only meant energy is found to exist in discrete quantities rather than as a continuum. What makes the quantum world mysterious is that these discrete-energy entities that we would normally call particles interfere with each other like waves, and this interference is a result of there being a certain probability of finding, say, a photon in a particular place. The interference of probability amplitudes is what makes quantum mechanics weird! More on that later, since it's a bit off our current subject of the Planck radiation box.
