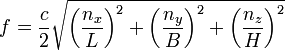EM modes of one-cubic-meter metallic box

Let’s look at a Planck box that has sides equal to one meter and ask what frequencies of “light” constitute the standing waves in such a box. With L = B = H = 1 meter in the frequency formula of my previous post, and of course c = the speed of light = 300,000,000 meters per second, which is divided by two, we have

f  = 150,000,00(n²_x + n²_y + n²_z)^1/2 hertz,

= (n²_x + n²_y + n²_z)^1/2 (1.5 X 10⁸) Hz.

This is meant to be a picture in mathematical form that shows the meaning of the word mode: put in integers for n_x, n_y, and n_z and you have chosen a particular mode, which you can see also corresponds to a particular frequency. But there are several modes for each frequency. For instance, the 1,1,0 mode has the same frequency as the 1,0,1 and 0,1,1 modes. This is the lowest frequency mode that can be supported by this box (for the 1,0,0, and 0,1,0 and 0,0,1 modes, wave motion doesn’t happen).

As you can see, this lowest frequency is 1.5 X 10⁸Hz.  My bad... That's gotta be multiplied by the square root of two, as you can see in the equation when you put in ones for two of the n's. The square root of two is 1.414. Putting that in gives the famous Manhattan area code, formerly the only one for Manhattan, in megahertz

f  = 2.12 X 10⁸ Hz = 212 X 10⁶ Hz = 212 MHz.

This is in the VHF (very high frequency) region where FM radio and lower-frequency TV stations broadcast (in fact this is almost exactly the carrier frequency of channel 13). UHF stations broadcast at higher frequencies, and cell phones transmit and receive at microwave frequencies which are even higher in frequency. All these are far below the frequencies of visible light.

This equation for frequencies in the one-cubic-meter box (approximately a one-cubic-yard box, for those of you not familiar with the meter) shows the normal modes of electromagnetic waves that can exist in the box.  What we really want to know is how such a box can produce electromagnetic (EM) waves in the first place, and what higher-frequency waves--even into the visible spectrum--can be produced.

You remember how, right?  The box is heated to a certain temperature and a spectrum of EM radiation is produced that is uniquely associated with that temperature:  the Planck spectrum. The Planck spectrum is observed when the walls of the box have equal rates of absorption and emission of electromagnetic energy, in other words when thermodynamic equilibrium is established. We’re getting back to thermodynamics now, and will be looking next at how temperature affects the frequencies produced by our cubic meter box.

Good description of a Planck radiation box

“The simplest way to model a radiating body is to regard it as a large number of linear oscillators (on the order of 10²³) performing simple harmonic motion. Since the particles undergoing the oscillations are, in general, charged particles, they will radiate electromagnetic waves. In the case of a cavity in thermal equilibrium, the electromagnetic energy density inside the cavity will equal the energy density of the atomic oscillators situated in the cavity walls. When the walls are raised to a higher temperature, the following events take place: more energy is put into existing oscillator modes by increasing their amplitudes, new modes corresponding to stiffer spring constants (higher frequencies) are excited, and the radiation density in the cavity is increased until a new equilibrium point is reached.”

--Elmer E. Anderson, from page 45 of Modern Physics and Quantum Mechanics, published in 1971 by W. B. Saunders Company.  It’s a good textbook, but I must confess I slightly edited this quotation. I didn't edit the last sentence, and for me that's the main explanatory part of the quote. My copy of the book is a complimentary copy sent by the publisher to Oswald F. “Mike” Schuette of the Physics & Astronomy Department at the U. of South Carolina. Professor Schuette died in 2000, thus allowing graduate students like me to obtain books from his office. We were given permission by Schuette’s family and the department, and it was suggested that we take any books we wanted, first come first served.  I got five or six books, including the transcript of J. Robert Oppenheimer's security hearings of 1954. 

What I like about Elmer's description is that he says increasing the temperature of the box puts more energy into existing modes and creates new modes at higher frequencies.  

I mentioned  in my previous post that a mode is almost the same thing as a single frequency, but not quite. The standing waves in the box, which are also called resonant frequencies or normal modes, are determined by the dimensions of the box.  The same idea in one dimension is shown by standing waves on a piece of string tied at both ends--a guitar or violin string for instance. These are the normal modes of the string and are determined by the length of the string. A single integer, usually expressed by our old friend n, multiplied by the speed of the waves on the string and divided by the twice the length of the string, determines the normal mode frequencies: f = n(v/2L).  

To put it in the language of music, when n=1 we have the fundamental frequency, and for n > 1 we have the harmonics. All the different strangely shaped waveforms produced by musical instruments and other sound sources are made of a linear superposition of pure tones--the fundamental and its harmonics--having different amplitudes. Mathematically, we're talking about Fourier analysis.

The same idea applies to light waves in the Planck box, but we have three integers because we have three dimensions, and a mode is determined by the different values these integers can have, ranging from zero to infinity. And the speed v in the equation above is now c, the speed of light. Our equation for the allowed frequencies is then a little more complicated:



where L, B and H are the box's dimensions in the x, y and z directions, respectively. For a light wave there are two independent polarizations that result in twice as many possible modes.

All of the above is classical physics, not quantum physics.  Planck's quantization of the energy of the waves is where the quantum of quantum mechanics comes in:  E = nhf, where E is energy, f is frequency, h is Planck's constant, and n is an integer that is now called "the number of photons in the mode." So when we say more energy is put into a mode, increasing its amplitude, that means n increases but f remains the same.

In addition, as Mr. Dr. Anderson says, new modes corresponding to higher frequencies are "excited" when the box is heated to a higher temperature.

Can there be different modes with the same energy?  Yes. To use easy-to-write frequencies, let's say we have two photons in a mode of frequency 100,000,000 Hz and one photon in a mode of frequency 200,000,000 Hz in our box. These modes of oscillation of the EM field in the box have the same energy but different frequencies. 

The quantum world would not be so mysterious if it only meant energy is found to exist in discrete quantities rather than as a continuum. What makes the quantum world mysterious is that these discrete-energy entities that we would normally call particles interfere with each other like waves, and this interference is a result of there being a certain probability of finding, say, a photon in a particular place.  The interference of probability amplitudes is what makes quantum mechanics weird!  More on that later, since it's a bit off our current subject of the Planck radiation box.