One thought is that a cubic-meter box such as I'm currently discussing would support resonant sound waves within human hearing range. The fundamental frequency would have a wavelength twice the length (or width or height, all the same) of the box. That wavelength is two meters, which corresponds to a frequency of 173.5 Hz, which is close to the F below middle C on a piano keyboard. The fundamental frequency of this F note is 174.6 Hz. And the wave we are talking about would be a pure sine wave, a single frequency wave. This is what "normal modes" are: single frequency waves. If higher-frequency sine waves (with lower "volume" or amplitude as physicists say) called harmonics are added to the fundamental, we can get the sound of a piano or of other instruments. For a good discussion with simple graphics, see The Physics Classroom website. It also shows visually why the fundamental standing wave or lowest acoustic normal-mode wave is one-half a wavelength instead of a full wavelength. And it should give you enough info to figure out what harmonics of this fundamental 173.5 Hz sound wave are supported in our cubic meter box.
If we raised the height of the box so that you could stand in it, it would be like a small shower stall, and you could find resonant frequencies by singing different frequencies and listening for the increase in sound volume when you hit the right notes. This brings up one difference in sound waves and electromagnetic waves in the box: the sound waves need to have a source inside the box (or a nearby source that resonates with the walls of the box). Heating the box doesn't make the whole thing vibrate acoustically, at least not so you could hear it.* Heating the box does make it produce more electromagnetic waves of higher frequency than it was producing at room temperature.
If we raised the height of the box so that you could stand in it, it would be like a small shower stall, and you could find resonant frequencies by singing different frequencies and listening for the increase in sound volume when you hit the right notes. This brings up one difference in sound waves and electromagnetic waves in the box: the sound waves need to have a source inside the box (or a nearby source that resonates with the walls of the box). Heating the box doesn't make the whole thing vibrate acoustically, at least not so you could hear it.* Heating the box does make it produce more electromagnetic waves of higher frequency than it was producing at room temperature.
That leads me to think about processes in the box that are normally not considered when discussing the Planck radiation spectrum. (I almost wrote "blackbox" radiation, which is actually a good description, too.) So, this will be an example of thinking outside the box about what's inside the box!
One thing to consider is thermionic emission, the emission of electrons from the walls of the box due to heating of the walls. Another thing to wonder about is the photoelectric effect: light hitting a clean metal surface and knocking electrons out of the surface. If the walls of our platinum box are covered with a soot-like material, then we don't have a clean metal surface. But if we think of both the thermionic effect and the photoelectric effect working together, then we can well imagine at high temperatures some electrons being ejected from the walls of the box into the open space inside the box. Free electrons! Yeeha! Come and get your free electrons!
Usually, for both thermionic emission and photoelectric emission, the emitted electrons are not free, because an applied electric field is used to cause the emission in the first place, so that once electrons are emitted they're in the presence of an electric field that makes them accelerate toward a positively charged plate (anode) connected to an external circuit for the electrons to flow through. The negative side of this circuit, the cathode, could be the heated metallic surface from which the electrons are emitted.
Emission of electrons from a hot cathode is the principle behind the old vacuum tubes that have mostly been replaced by transistors, and of old-style TV picture tubes. They're called cathode-ray tubes, CRTs, remember? I still have one. The cathode-ray technique is also used to generate X-rays for research and medical testing. Using an accelerating voltage in the 10,000 to 100,000 volt range, high-speed electrons hitting atoms in the anode generate X-rays.
Another of my thoughts about the Planck black-body radiation box is related to the type of object it is supposed to simulate: an object, or a surface, or in the usual parlance, a body capable of absorbing all the radiation that hits it. This perfect absorber is, by Kirchhoff's law of thermal radiation, also a perfect emitter. Contrast such a body with "dark matter". Dark matter seems to be an example of a perfect non-emitter of radiation, which, if Kirchhoff's law applies to it, means it's also a perfect non-absorber. Opposite of black-body!
And what about a comparison to that other true-black object in physics, the black hole? It does absorb all the radiation impinging on it, and, except for particle-antiparticle Hawking radiation, emits none of the absorbed radiation
Dark matter is postulated to exist in a halo near the borders of some galaxies, and black holes are postulated to be, and experimentally indicated to be,but not positively proven to be, at the centers of some galaxies. Because of this, the mass of a black hole at the center a galaxy can't account for the rotational speed "profile" of the galaxy like dark matter can. Some scientists still argue against the existence of black holes, and even more are skeptical about the existence of dark matter.
Usually, for both thermionic emission and photoelectric emission, the emitted electrons are not free, because an applied electric field is used to cause the emission in the first place, so that once electrons are emitted they're in the presence of an electric field that makes them accelerate toward a positively charged plate (anode) connected to an external circuit for the electrons to flow through. The negative side of this circuit, the cathode, could be the heated metallic surface from which the electrons are emitted.
Emission of electrons from a hot cathode is the principle behind the old vacuum tubes that have mostly been replaced by transistors, and of old-style TV picture tubes. They're called cathode-ray tubes, CRTs, remember? I still have one. The cathode-ray technique is also used to generate X-rays for research and medical testing. Using an accelerating voltage in the 10,000 to 100,000 volt range, high-speed electrons hitting atoms in the anode generate X-rays.
Another of my thoughts about the Planck black-body radiation box is related to the type of object it is supposed to simulate: an object, or a surface, or in the usual parlance, a body capable of absorbing all the radiation that hits it. This perfect absorber is, by Kirchhoff's law of thermal radiation, also a perfect emitter. Contrast such a body with "dark matter". Dark matter seems to be an example of a perfect non-emitter of radiation, which, if Kirchhoff's law applies to it, means it's also a perfect non-absorber. Opposite of black-body!
And what about a comparison to that other true-black object in physics, the black hole? It does absorb all the radiation impinging on it, and, except for particle-antiparticle Hawking radiation, emits none of the absorbed radiation
Dark matter is postulated to exist in a halo near the borders of some galaxies, and black holes are postulated to be, and experimentally indicated to be,
*well, heating does increase the internal vibrations--which are acoustic vibrations or sound waves--in the walls of the box, a related subject I'll discuss later! These acoustic vibrations in the solid walls are similar to what's happening with the confined electromagnetic waves in the empty space of the box.

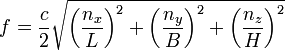
 power law, which matches experiment. This modification is called the
power law, which matches experiment. This modification is called the